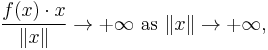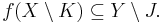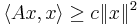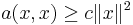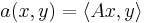Coercive function
In mathematics, a coercive function is a function that "grows rapidly" at the extremes of the space on which it is defined. More precisely, a function f : Rn → Rn is called coercive if
where " " denotes the usual dot product and
" denotes the usual dot product and 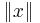 denotes the usual Euclidean norm of the vector x.
denotes the usual Euclidean norm of the vector x.
More generally, a function f : X → Y between two topological spaces X and Y is called coercive if for every compact subset J of Y there exists a compact subset K of X such that
The composition of a bijective proper map followed by a coercive map is coercive.
Coercive operators and forms
A self-adjoint operator 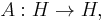 where
where  is a real Hilbert space, is called coercive if there exists a constant
is a real Hilbert space, is called coercive if there exists a constant 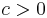 such that
such that
for all  in
in 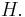
A bilinear form 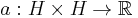 is called coercive if there exists a constant
is called coercive if there exists a constant 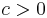 such that
such that
for all  in
in 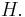
It follows from the Riesz representation theorem that any symmetric ( for all
for all 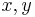 in
in  ), continuous (
), continuous (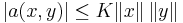 for all
for all 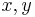 in
in  and some constant
and some constant  ) and coercive bilinear form
) and coercive bilinear form  has the representation
has the representation
for some self-adjoint operator 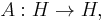 which then turns out to be a coercive operator. Also, given a coercive operator self-adjoint operator
which then turns out to be a coercive operator. Also, given a coercive operator self-adjoint operator 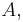 the bilinear form
the bilinear form  defined as above is coercive.
defined as above is coercive.
One can also show that any self-adjoint operator 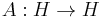 is a coercive operator if and only if it is a coercive function (if one replaces the dot product with the more general inner product in the definition of coercivity of a function). The definitions of coercivity for functions, operators, and bilinear forms are closely related and compatible.
is a coercive operator if and only if it is a coercive function (if one replaces the dot product with the more general inner product in the definition of coercivity of a function). The definitions of coercivity for functions, operators, and bilinear forms are closely related and compatible.
References
- Renardy, Michael and Rogers, Robert C. (2004). An introduction to partial differential equations (Second edition ed.). New York, NY: Springer-Verlag. pp. xiv+434. ISBN 0-387-00444-0.
- Bashirov, Agamirza E (2003). Partially observable linear systems under dependent noises. Basel; Boston: Birkhäuser Verlag. ISBN 081766999X.
- Gilbarg, D.; Trudinger, N. (2001). Elliptic partial differential equations of second order, 2nd ed. Berlin; New York: Springer. ISBN 3540411607.
This article incorporates material from Coercive Function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.